The Blessing and Curse of Dimensionality in Safety Alignment
The Blessing and Curse of Dimensionality in Safety Alignment
(发表于Second Conference on Language Modeling 2025)
一、论文概览
1. 核心问题
大语言模型(LLMs)的广泛应用推动了安全对齐研究的发展,而LLMs的成功依赖于参数规模的扩大,这伴随着隐藏维度的增长。论文提出核心假设:隐藏维度的增加既是LLMs的“祝福”(支持复杂概念的线性表示以提升性能),也是“诅咒”(高维激活空间中的线性结构易被“激活工程”(如ActAdd越狱攻击)利用,破坏安全对齐),即维度在LLM安全对齐中存在“双刃剑”效应。
2. 主要贡献
- 维度与线性表示的关联分析:通过系统实验(线性探针)和可视化(PCA),验证了“抽象概念(如安全、情绪)的线性表示依赖足够大的隐藏维度”,并揭示该关联对安全对齐的影响。
- 越狱方法的理论洞察:从学习理论(Rademacher复杂度、VC维)出发,分析了利用激活空间线性结构的越狱攻击(如ActAdd、Ablation)与模型隐藏维度的关系,证明高维度会提升线性攻击的有效性。
- 新型防御微调方法:提出两种基于低维投影的微调策略——FJLT(快速约翰逊-林登施特劳斯变换) 和Bottleneck(线性自编码器瓶颈),在保留安全对齐信息的同时,破坏易被攻击的线性结构,显著降低越狱 susceptibility。
3. 研究方法
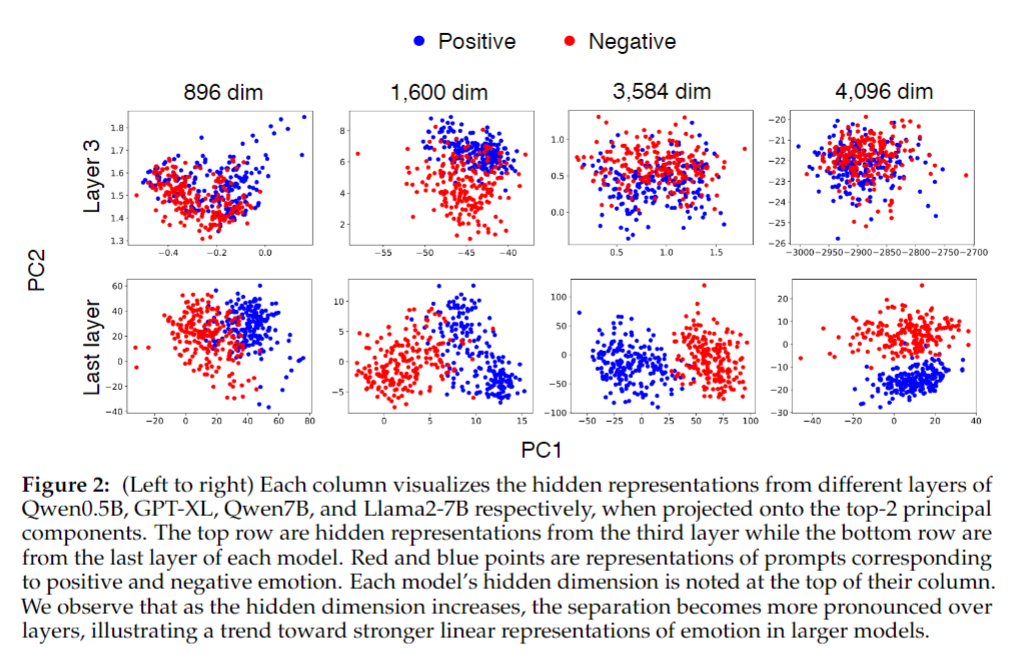
- 可视化验证:用主成分分析(PCA)将不同规模模型(如Qwen0.5B、GPT-XL、Qwen7B)的激活投影到前2个主成分,观察“正负情绪”“安全/有害”等概念的线性可分性。
- 线性探针实验:训练线性分类器(探针),基于模型激活预测“情绪正负”“指令安全与否”,验证高维模型对抽象概念的线性表示能力更强。
- 理论分析:基于Rademacher复杂度推导维度与线性假设类容量的关系(定理1:$\mathfrak{R}_N(\mathcal{F}) \lesssim L\sqrt{D/N}$),证明降维可降低线性攻击的有效性。
- 防御方法设计与实验:在Llama2-7B-Chat、Gemma-1.1-7B-IT、Qwen2-7B-Instruct三种模型上实现FJLT和Bottleneck,以“拒绝率”(有害指令的拒绝比例)、“安全分数”(Llama Guard 2判定的安全响应比例)、“困惑度(PPL)”(良性指令的响应连贯性)为指标,评估对ActAdd、Ablation越狱的防御效果。
二、论文各章节详解
1. 引言(Introduction)
- LLMs的应用与安全需求:LLMs在自然语言生成、逻辑推理、摘要等领域广泛应用,但自主性提升导致“有害响应”风险加剧;安全对齐的目标是让模型对无害指令提供帮助,对有害指令拒绝响应,常用方法包括监督微调(SFT)、基于人类反馈的强化学习(RLHF)、直接偏好优化(DPO)。
- 线性表示假设与维度问题:现有研究认为LLMs中抽象概念(如安全、真理)以“激活空间中的线性方向”存在(即“线性表示假设”),且该结构仅在高维大模型中涌现;这一结构可被激活工程利用(如修改激活引导模型行为),但此前缺乏对“维度-线性表示-安全对齐”关联的系统分析。
- 研究目标与贡献:明确三个核心贡献(见“主要贡献”),旨在阐明维度的双重作用,并提出防御策略。
2. 背景(Background)
(1)符号定义
- prompt-response对:$(x,y)\sim\mathcal{D}$($\mathcal{D}$为数据分布),$y_{<t}$表示$y$的前$t-1$个token,$y_t$为第$t$个token;
- LLM表示:$\pi_\theta$(参数为$\theta$的基础模型),$\pi_{aligned}$(经过对齐的Chat/Instruct模型);
- 下一个token概率:$\pi(y_t|x,y_{<t})$(给定$x$和$y_{<t}$时生成$y_t$的概率向量)。
(2)线性表示(Linear Representations)
-
抽象概念(如情绪、安全)在激活空间中表现为“线性方向”(称为“引导向量”),通过“对比prompt的激活差”获取:例如,收集“正情绪prompt”和“负情绪prompt”的激活,计算均值差即为“情绪引导向量”(示例见图1)。

-
复杂概念(如安全)的线性表示仅在高维模型中涌现,低维模型无法形成清晰线性结构。
(3)激活工程越狱(Jailbreaking via Activation Engineering)
- ActAdd:计算“有害prompt激活均值”与“无害prompt激活均值”的差($r_{i}^{(\ell)}=\mu_i^{(\ell)}-v_i^{(\ell)}$),将该向量添加到无害prompt的激活中,诱导模型生成有害内容;
- Ablation:将“安全引导向量”归一化为单位向量$\hat{r}{i}^{(\ell)}$,通过投影移除激活中该方向的分量($x_i^{(\ell)\prime}=x_i^{(\ell)}-\hat{r}{i}^{(\ell)}(\hat{r}_{i}^{(\ell)\top}x_i^{(\ell)})$),破坏安全对齐,导致模型拒绝无害指令。
(4)Transformer架构
- 注意力机制:给定层$\ell$的隐藏表示$x^{(\ell)}$,通过线性变换得到查询($Q=x^{(\ell)}W_Q^\top$)、键($K=x^{(\ell)}W_K^\top$)、值($V=x^{(\ell)}W_V^\top$);
- 注意力输出:$\tilde{x}^{(\ell)}=x^{(\ell)}+softmax\left(\frac{QK^\top}{\sqrt{D}}\right)V$($D$为隐藏维度);
- 层输出:$x^{(\ell+1)}=\tilde{x}^{(\ell)}+MLP(\tilde{x}^{(\ell)})$(MLP为多层感知机)。
3. 线性可分性悖论(The Paradox of Linear Separability)
(1)线性可分性验证
-
激活可视化(PCA):图2显示,低维模型(如Qwen0.5B,896维)的最终层中“正负情绪”prompt的激活投影高度重叠;高维模型(如Llama2-7B,4096维)的最终层中两类激活形成清晰聚类,线性可分性显著增强。
-
线性探针实验:图3显示,当模型隐藏维度超过2000时,线性探针对“情绪正负”的分类准确率从~0.6提升至~0.7,证明高维模型对抽象概念的线性表示能力更强。
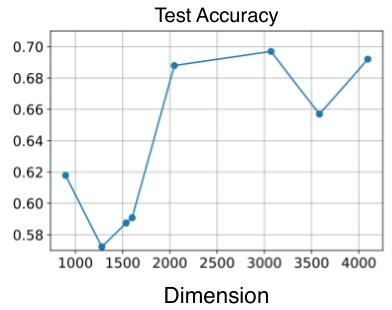
(2)线性可分性悖论
- 核心结论:模型规模扩大(维度增加)虽提升性能,但也使线性结构更易被越狱攻击利用,即“维度既是性能提升的祝福,也是安全风险的诅咒”。
(3)学习理论视角
- Rademacher复杂度分析:Rademacher复杂度衡量假设类(如线性分类器)的“拟合能力”,论文证明线性假设类的Rademacher复杂度满足$\mathfrak{R}_N(\mathcal{F}) \lesssim L\sqrt{\frac{D}{N}}$(定理1),其中$D$为输入维度,$N$为样本量;
- 降维的防御逻辑:降维($k<D$)可使Rademacher复杂度按$\sqrt{D}$的速率降低,导致线性分类器(如攻击用的引导向量学习)更难找到有效方向,从而削弱ActAdd等攻击。
4. 抵御引导向量的方法(Guarding Against Steering Vectors)
(1)FJLT方法(Fast Johnson–Lindenstrauss Transform)
- 核心思想:利用FJLT(快速约翰逊-林登施特劳斯变换)将注意力层的Q和K投影到低维子空间($K<D$),在保留欧氏距离的同时破坏线性结构。
- 实现细节:为每层注意力的单个头(超参数)构造投影矩阵$\Phi^{(\ell)}\in\mathbb{R}^{D×K}$,投影后Q和K为$Q_{proj}=Q\Phi^{(\ell)}$、$K_{proj}=K\Phi^{(\ell)}$,注意力输出为$\tilde{x}^{(\ell)}=x^{(\ell)}+softmax\left(\frac{Q_{proj}K_{proj}^\top}{\sqrt{D}}\right)V$。
- 微调目标:采用token级约束目标,最小化FJLT模型与对齐模型的分布差异:
$$min {\theta}\left{\mathbb{E}{(x, y) \sim \mathcal{D}}-\sum_{t=1}^{|y|} \frac{2}{\beta_{t}} log \left[\sigma\left(\beta_{t} log \frac{\pi_{\theta}\left(y_{t} | x, y_{<t}\right)}{\pi_{aligned }\left(y_{t} | x, y_{<t}\right)}\right)\right]\right}$$
其中$\sigma(x)=\frac{1}{1+\exp^{-x}}$(sigmoid函数),$\beta_t$为正则化超参数。 - 局限性:在专业数据集(如SQL Create Context、GSM8k)上性能下降,因过度压缩导致概念丢失。
(2)Bottleneck方法
- 核心思想:在连续两层间插入“线性自编码器”,形成“压缩-重构”瓶颈,局部降维以减少线性结构,同时避免全局压缩导致的信息丢失。
- 实现细节:插入层$\ell$后,激活经过$x_{compressed}^{(\ell)}=\sigma(x^{(\ell)}W_{down}W_{up})$($W_{down}\in\mathbb{R}^{D×K}$、$W_{up}\in\mathbb{R}^{K×D}$为压缩/重构权重,$\sigma$为激活函数),再输入层$\ell+1$。
- 微调目标:结合“有害指令拒绝数据集$\mathcal{D}_P$”和“良性指令安全数据集$\mathcal{D}B$”的损失,平衡安全与效用:
$$min {\theta} \mathbb{E}{(x, y) \sim \mathcal{D}P}\left[-log \pi{\theta}(y | x)\right]+\alpha \mathbb{E}{(x, y) \sim \mathcal{D}B}\left[-log \pi{\theta}(y | x)\right]$$
其中$\alpha$为正则化超参数,控制$\mathcal{D}_B$的影响。
5. 实验(Experiments)
(1)实验设置
- 模型与数据集:三种对齐模型(Llama2-7B-Chat、Gemma-1.1-7B-IT、Qwen2-7B-Instruct),评估数据集为JailbreakBench(有害指令)、Alpaca(良性指令),微调数据集为$\mathcal{D}_P$(有害指令+拒绝响应)、$\mathcal{D}_B$(良性指令+安全响应);
- 硬件与重复次数:8个H100 GPU,结果为5次实验平均值;
- 评估指标:
- 有害指令:拒绝率(↑)、安全分数(↑);
- 良性指令:拒绝率(↓)、困惑度(PPL,↓,衡量响应连贯性)。
(2)FJLT实验结果(表1)
- 对比“基线模型”“仅微调模型(FT)”“FJLT模型”:ActAdd攻击后,FJLT模型的有害指令拒绝率显著提升(如Llama2-7B-Chat-FJLT为0.94±0.06,基线仅0.03),安全分数接近基线水平(0.96±0.03 vs 0.99),良性指令拒绝率降低(0.63±0.03 vs 1.00),证明FJLT有效抵御越狱且保留安全对齐。
(3)Bottleneck实验结果(表2)
- Bottleneck模型表现更优:Llama2-7B-Chat-Bottleneck在ActAdd攻击后,有害指令拒绝率达0.95±0.02,安全分数0.97±0.01,良性指令拒绝率仅0.30±0.03(70%良性指令可正常响应),且在SQL Create Context、GSM8k等专业数据集上效用接近基线(表13),克服了FJLT的局限性。
(4)概念保留分析(图4)
- PCA显示:FJLT模型虽破坏“安全”的线性表示,但也扭曲“真理”“情绪”的概念结构;Bottleneck模型仅破坏“安全”的线性表示,同时保留“真理”“情绪”的清晰聚类,证明其在“防御”与“效用”间的平衡更优。
6. 相关工作(Related Work)
- 概念擦除:INLP(迭代零空间投影)、LEACE(完美线性概念擦除)等方法旨在移除表示中的特定属性,但多聚焦线性结构,且难以平衡“擦除”与“效用”;
- 安全对齐:Zhou et al.(2024a)指出标准对齐方法的局限性,Li et al.(2025)发现中间层存在隐性安全机制,但均未关注维度的作用;
- 本文差异:首次系统分析“维度-线性表示-安全对齐”的关联,从理论+实验验证维度的双重作用,提出的降维方法针对性抵御线性越狱。
7. 结论(Conclusion)
- 核心发现:LLMs的高维度是“双刃剑”——支持复杂概念的线性表示以提升性能(祝福),但线性结构易被越狱攻击利用(诅咒);
- 方法有效性:FJLT和Bottleneck通过低维投影破坏安全相关的线性结构,显著降低ActAdd、Ablation越狱的成功率,且Bottleneck能更好保留模型效用;
- 未来方向:需设计“基于语义的投影方法”,进一步平衡防御效果与概念保留。
8. 补充内容(Supplement)
- 理论背景:补充多头注意力细节、JL引理(存在低维映射保留 pairwise 距离)、FJLT的矩阵构造(稀疏矩阵P+沃尔什-哈达玛矩阵H+对角矩阵D)、命题1(正态分布特征向量的Rademacher复杂度边界)的证明;
- 实验细节:ActAdd/Ablation的具体实现步骤、超参数设置(如学习率、epoch、投影维度K)、开源模型与数据集链接;
- 消融实验:
- FJLT的注意力头选择:仅投影第0个头时效果最优(表6),多头部投影会导致模型过度拒绝(表7);
- Bottleneck的层位置:插入第0层(早期层)效果最好,插入后期层会丢失已提取的复杂信息(表8);
- $\alpha$的敏感性:$\alpha$在0.8-1.2范围内变化时,模型性能稳定(表10),无需精细调参;
- 局限性:对非线性攻击(如GCG)防御效果有限(Llama2-7B-Chat-FJLT的GCG攻击成功率53%,基线42%),依赖“安全概念线性表示”的假设,需模型特定的$\mathcal{D}_B$数据集。
三、一句话总结
论文假设LLMs高维隐藏表示既是安全对齐的“祝福”(支持复杂概念线性表示以提升性能)也是“诅咒”(线性结构易被ActAdd等越狱攻击利用),通过PCA可视化、线性探针验证了维度与线性表示的正相关,用Rademacher复杂度($\mathfrak{R}_N(\mathcal{F}) \lesssim L\sqrt{D/N}$)提供理论支撑,提出FJLT和Bottleneck两种低维投影微调方法,在三种主流LLM上实验表明两种方法能显著提升对ActAdd越狱的抵御能力(如Llama2-7B-Chat的两种方法有害指令拒绝率均超0.94),且Bottleneck能保留模型在专业任务上的效用,最终证实维度在LLM安全对齐中的双重作用,为抵御线性越狱攻击提供有效策略。